Plaits engines
This list was adapted from the original Plaits manual, with some edits to match Tidal’s parameter implementation.
The engine parameter (0-15) can be set to select one of the models listed below.
All engines accept the harm, timbre and morph parameters, which have specific ways to shape the sound in each engine. The original Plaits module has an additional AUX output which features a distinct rendering of the original sound; in Tidal, you can set the mode parameter to 1 to get the equivalent to the AUX output.
0: Pair of classic waveforms
Virtual-analog synthesis of classic waveforms.
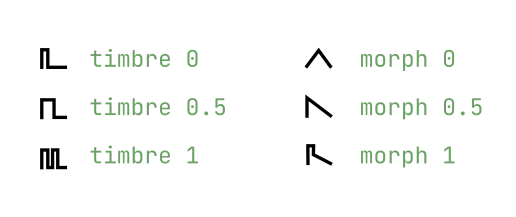
| parameter | effect |
|---|---|
| harm | detuning between the two waves |
| timbre | variable square, from narrow pulse to full square to hardsync formants |
| morph | variable saw, from triangle to saw with an increasingly wide notch (Braids’ CSAW) |
| mode 1 | sum of two hardsync’ed waveforms, the shape of which is controlled by morph and detuning by harm |
A narrow pulse or wide notch results in silence! Use this trick if you want to silence one of the two oscillators, to get a variable square or variable saw.
1: Waveshaping oscillator
An asymmetric triangle processed by a waveshaper and a wavefolder. Sounds familiar? That’s the same signal processing chain as in Tides, when it runs at audio rate!
| parameter | effect |
|---|---|
| harm | waveshaper waveform |
| timbre | wavefolder amount |
| morph | waveform asymmetry |
| mode 1 | variant employing another wavefolder curve, as available in Warps |
2: Two operator FM
Two sine-wave oscillators modulating each other’s phase.
| parameter | effect |
|---|---|
| harm | frequency ratio |
| timbre | modulation index |
| morph | feedback, in the form of operator 2 modulating its own phase (past 0.5, rough!) or operator 1’s phase (before 0.5, chaotic!) |
| mode 1 | sub-oscillator |
Note: Set morph to 0 to get the same range of sounds as Braids’ WTFM. Set it to 1 to recreate the same sounds as Braids’ FBFM. A gentler palette equivalent to Braids’ FM is found with morph at 0.5.
3: Granular formant oscillator
Simulation of formants and filtered waveforms through the multiplication, addition and synchronization of segments of sine waves.
| parameter | effect |
|---|---|
| harm | frequency ratio between formant 1 and 2 |
| timbre | formant frequency |
| morph | formant width and shape; this controls the shape of the window by which a sum of two synchronized sine oscillators is multiplied |
| mode 1 | simulation of filtered waveforms by windowed sine waves – a recreation of Braids’ Z*** models. harm controls the filter type (peaking, LP, BP, HP), with smooth variation from one response to another |

4: Harmonic oscillator
An additive mixture of harmonically-related sine waves.
| parameter | effect |
|---|---|
| harm | number of bumps in the spectrum; starts with one big bump, and progressively adds ripples around it |
| timbre | index of the most prominent harmonic; this control is somewhat similar to the cutoff frequency of a band-pass filter |
| morph | bump shape – from flat and wide to peaked and narrow; this control is somewhat similar to the resonance of a band-pass filter |
| mode 1 | variant including only the subset of harmonics present in the drawbars of a Hammond organ (frequency ratios of 1, 2, 3, 4, 6, 8, 10 and 12) |
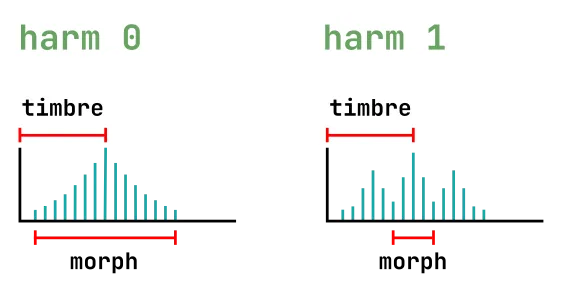
5: Wavetable oscillator
Four banks of 8x8 waveforms, accessed by row and column, with or without interpolation.
| parameter | effect |
|---|---|
| harm | sets the active bank (read below) |
| timbre | row index; within a row, the waves are sorted by spectral brightness (except for bank D which is a mess!) |
| morph | column index |
| mode 1 | low-fi (5-bit) output |
There are 4 interpolated banks followed by the same 4 banks, in reverse order, without interpolation.
- Bank A: harmonically poor waveforms obtained by additive synthesis (sine harmonics, drawbar organ waveforms).
- Bank B: harmonically rich waveforms obtained by formant synthesis or waveshaping.
- Bank C: wavetables from the Shruthi-1 / Ambika, sampled from classic wavetable or ROM playback synths.
- Bank D: a joyous semi-random permutation of waveforms from the other 3 banks.
6: Chords
Four-note chords, played by virtual analogue or wavetable oscillators. The virtual analogue oscillators emulate the stack of harmonically-related square or sawtooth waveforms generated by vintage string&organ machines.
| parameter | effect |
|---|---|
| harm | chord type |
| timbre | chord inversion and transposition |
| morph | waveform; values until 0.5 go through a selection of string-machine like raw waveforms (different combinations of the organ and string “drawbars”), and above 0.5 it scans a small wavetable containing 16 waveforms |
| mode 1 | root note of the chord |
The proper values for harm (chord type) are
| value | chord |
|---|---|
| 0.00 - 0.08 | octave |
| 0.09 - 0.17 | 5 |
| 0.18 - 0.26 | sus4 |
| 0.27 - 0.36 | m |
| 0.37 - 0.46 | m7 |
| 0.47 - 0.56 | m9 |
| 0.57 - 0.66 | m11 |
| 0.67 - 0.75 | M 6/9 |
| 0.76 - 0.85 | M9 |
| 0.86 - 0.95 | M7 |
| 0.96 - 1 | M |
7: Vowel and speech synthesis
A collection of speech synthesis algorithms.
| parameter | effect |
|---|---|
| harm | crossfades between formant filtering, SAM, and LPC vowels, then goes through several banks of LPC words |
| timbre | species selection, from Daleks to chipmunks. How does it work? This parameter either shifts the formants up or down independently of the pitch; or underclocks/overclocks the emulated LPC chip (with appropriate compensation to keep the pitch unchanged) |
| morph | phoneme or word segment selection. When harm is greater than (0.4? original docs say knob at 11o’clock), a list of words can be scanned through |
| mode 1 | unfiltered vocal cords’ signal |
8: Granular cloud
A swarm of 8 enveloped sawtooth waves.
| parameter | effect |
|---|---|
| harm | amount of pitch randomization |
| timbre | grain density |
| morph | grain duration and overlap; when set to 1, the grains merge into each other: the result is a stack of eight randomly frequency-modulated waveforms |
| mode 1 | variant with sine wave oscillators |
To get a nice “supersaw” waveform, try a moderate amount of pitch randomization and grain density, with full grain overlap.
9: Filtered noise
Variable-clock white noise processed by a resonant filter. The cutoff frequency of the filter is controlled by freq. This allows proper tracking!
| parameter | effect |
|---|---|
| harm | filter response, from LP to BP to HP |
| timbre | clock frequency |
| morph | filter resonance |
| mode 1 | variant employing two band-pass filters, with their separation controlled by harm |
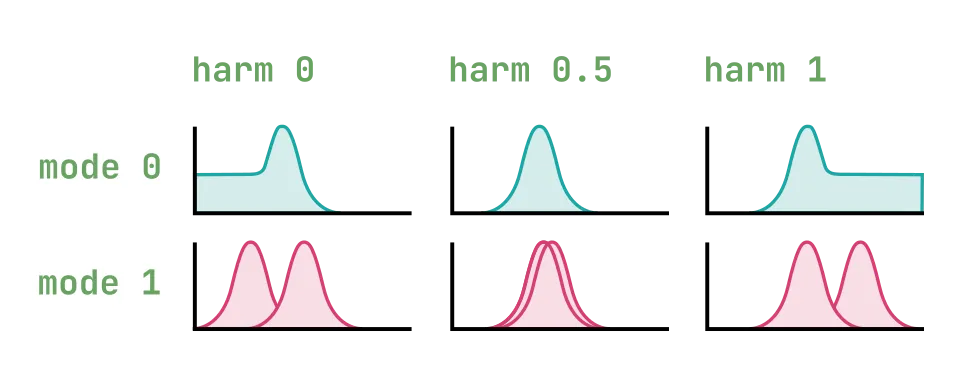
10: Particle noise
Dust noise processed by networks of all-pass or band-pass filters.
| parameter | effect |
|---|---|
| harm | amount of frequency randomization |
| timbre | particle density |
| morph | filter type – reverberating all-pass network before 0.5, then increasingly resonant band-pass filters |
| mode 1 | raw dust noise |
11: Inharmonic string modeling
No info on the original docs
12: Modal resonator
For your own pleasure, a mini-Rings! Refer to the Rings section for more information about modulated/inharmonic string synthesis, and modal resonators.
When the TRIG input is not patched, the string/resonator is excited by dust (particle) noise. Otherwise, the string is excited by a short burst of filtered white noise, or by a low-pass filtered click. (FIXME: what does the TRIG input equate to in Tidal?)
| parameter | effect |
|---|---|
| harm | amount of inharmonicity, or material selection |
| timbre | excitation brightness and dust density |
| morph | decay time (energy absorption) |
| mode 1 | raw exciter signal |
Note that Plaits uses a less powerful processor than Rings, and is thus limited to 3 voices of polyphony in inharmonic string modeling mode, and 1 voice of polyphony with 24 partials in modal resonator mode. Plaits does not allow you to control the position of the excitation, which is set to 25% of the length of the string/bar/tube.
13: Analog bass drum model
No fancy acronyms or patented technology here… Just behavioral simulation of circuits from classic drum machines! The drum machine employs a bridged T-network excited by a nicely shaped pulse.
| parameter | effect |
|---|---|
| harm | attack sharpness and amount of overdrive |
| timbre | brightness |
| morph | decay time |
| mode 1 | frequency-modulated triangle VCO, turned into a sine with a pair of diodes, and shaped by a dirty VCA |
Without any signal patched to the TRIG input, a continuous tone is produced. Not particularly useful, but its amplitude can still be modulated by morph and CV input (FIXME: equivalent to CV input in Tidal?).
14: Analog snare drum model
The generator employs a bunch of bridged T-networks, one for each mode of the shell, excited by a nicely shaped pulse; plus some band-pass filtered noise.
| parameter | effect |
|---|---|
| harm | balance of the harmonic and noisy components |
| timbre | balance between the different modes of the drum |
| morph | decay time |
| mode 1 | a pair of frequency-modulated sine VCO, mixed with high-pass filtered noise |
15: Analog hi-hat model
A bunch of square oscillators generate a harsh, metallic tone. The resulting signal is mixed with clocked noise, sent to a HPF, then to a VCA. It uses 6 square oscillators and a dirty transistor VCA.
| parameter | effect |
|---|---|
| harm | balance of the metallic and filtered noise |
| timbre | high-pass filter cutoff |
| morph | decay time |
| mode 1 | three pairs of square oscillators ring-modulating each other, and a clean, linear VCA |